Mặt cầu

Định nghĩa

Tập hợp các điểm $M$ trong không gian cách điểm $O$ một khoảng không đổi bằng $R, (R>0)$ được gọi là mặt cầu tâm $O$ bán kính $R$

Ký hiệu: $S(O;R)$

Khi đó $S(O;R)=\{M|MO=R\}$

+) $C,D\in S(O;R)$ thì $CD$ được gọi là dây cung của mặt cầu đó

+) Dây cung đi qua tâm được gọi là đường kính của mặt cầu

+) Một mặt cầu được xác định khi biết tâm và bán kính

---

Điểm nằm trong, nằm ngoài mặt cầu

Cho mặt cầu $S(O;R)$

+) Nếu $OA >R$ thì điểm $A$ nằm ngoài mặt cầu

+) Nếu $OA <R$ thì điểm $A$ nằm trong mặt cầu

+) Nếu $OA=R$ thì điểm $A$ nằm trên mặt cầu

---

Giao của mặt cầu và mặt phẳng

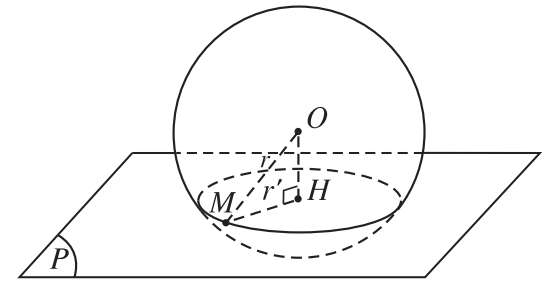
Cho mặt cầu $S(O;R)$ và mặt phẳng $(P)$

+) Nếu $d(O;(P))>R$ thì mặt phẳng $(P)$ không cắt mặt cầu

+) Nếu $d(O;(P))=R$ thì mặt phẳng $(P)$ tiếp xúc với mặt cầu

+) Nếu $d(O;(P))<R$ thì mặt phẳng $(P)$ cắt mặt cầu theo giao tuyến là một đường tròn

---

Giao của mặt cầu và đường thẳng

Cho mặt cầu $S(O;R)$ và đường phẳng $\Delta$

+) Nếu $d(O;\Delta)>R$ thì đường thẳng $\Delta$ không cắt mặt cầu

+) Nếu $d(O;\Delta)=R$ thì đường thẳng $\Delta$ tiếp xúc vói mặt cầu

+) Nếu $d(O;\Delta)<R$ thì đường thẳng $\Delta$ cắt mặt cầu tại hai điểm phân biệt

Nhận xét

Qua một điểm nằm trên mặt cầu có vô số tiếp tuyến của mặt cầu đi qua điểm đó

Qua một điểm nằm ngoài mặt cầu có vô số tiếp tuyến của mặt cầu đi qua điểm đó

---

Diện tích mặt cầu, thể tích khối cầu

Diện tích mặt cầu

$$S=4\pi R^2$$

Thể tích khối cầu

$$V=\frac{4}{3}\pi R^3$$

---

Chóp, lăng trụ nội tiếp mặt cầu

Chóp

+) Điều kiện để một hình chóp nội tiếp mặt cầu là đáy của hình chóp là một đa giác nội tiếp được đường tròn

Cách xác định mặt cầu ngoại tiếp hình chóp

Bước 1. Xác định trục $d$ của đa giác đáy (trục đa giác đáy là đường thẳng đi qua tâm của đa giác đáy và vuông góc với mặt phẳng đáy)

Bước 2. Xác định mặt phẳng trung trực $(P)$ của một cạnh bên bất kỳ

Khi đó giao của $d$ và $(P)$ chính là tâm của mặt cầu ngoại tiếp hình chóp

Lăng trụ

+) Điều kiện để một hình lăng trụ nội tiếp được mặt cầu là hình lăng trụ là lăng trụ đứng và có đáy là đa giác nội tiếp được đường tròn

Công thức mở rộng

Mặt cầu ngoại tiếp hình hộp chữ nhật có ba kích thước $a,b,c$ có bán kính $r$ là:

$$r=\frac{1}{2}\sqrt{a^2+b^2+c^2}$$