TÍCH PHÂN BỘI HAI, TÍCH PHÂN KÉP, ĐỔI THỨ TỰ LẤY TÍCH PHÂN, BÀI TẬP CÓ LỜI GIẢI CHI TIẾT

If you break someone's heart and they still talk to you with the same excitement and respect, believe me, they really love you

MIỀN $D$ LÀ HÌNH CHỮ NHẬT

Đối với miền $D$ là hình chữ nhật thì ta có thể tính tích phân theo biến nào trước vẫn được

Câu 1. Tính $\displaystyle I=\iint\limits_{D}{\left( x{{y}^{2}}+y \right)dxdy}$ với $D=\left[ 0;1 \right]\times \left[ 0;2 \right]$

$\displaystyle I=\iint\limits_{D}{\left( x{{y}^{2}}+y \right)dxdy}=\int\limits_{0}^{1}{dx}\int\limits_{0}^{2}{\left( x{{y}^{2}}+y \right)dy}$

$\displaystyle =\int\limits_{0}^{1}{\left[ \left. \left( \frac{x{{y}^{3}}}{3}+\frac{{{y}^{2}}}{2} \right) \right|_{0}^{2} \right]dx}$

$\displaystyle =\int\limits_{0}^{1}{\left( \frac{8}{3}x+2 \right)dx}=\frac{10}{3}$

Câu 2. Tính $\displaystyle I=\iint\limits_{D}{{{x}^{2}}\left( x-y \right)dxdy}$ với $D=\left[ 0;1 \right]\times \left[ 0;1 \right]$

$\displaystyle I=\int\limits_{0}^{1}{dx}\int\limits_{0}^{1}{{{x}^{2}}\left( y-x \right)dy}$

$\displaystyle =\int\limits_{0}^{1}{dx}\int\limits_{0}^{1}{\left( {{x}^{2}}y-{{x}^{3}} \right)dy}$

$\displaystyle =\int\limits_{0}^{1}{\left[ \left. \left( \frac{{{x}^{2}}{{y}^{2}}}{2}-{{x}^{3}}y \right) \right|_{0}^{1} \right]dx}$

$\displaystyle =\int\limits_{0}^{1}{\left( \frac{{{x}^{2}}}{2}-{{x}^{3}} \right)dx}$

$\displaystyle =\left. \left( \frac{{{x}^{3}}}{6}-\frac{{{x}^{4}}}{4} \right) \right|_{0}^{1}=-\frac{1}{12}$

---

MIỀN $D$ GIỚI HẠN BỞI CÁC ĐƯỜNG (KHÔNG PHẢI HÌNH CHỮ NHẬT)

Câu 3. Tính $\displaystyle \iint\limits_{D}{\left( x{{y}^{2}}+y \right)dxdy}$ với $D$ được giới hạn bởi các đường $y={{x}^{2}}$, $y=2-x$

+) Biểu diễn miền $D$ trên $Oxy$

+) Viết lại $D:\left\{ \begin{align} & -2\le x\le 1 \\ & {{x}^{2}}\le y\le 2-x \\ \end{align} \right.$

Vậy

$\displaystyle I=\iint\limits_{D}{\left( x{{y}^{2}}+y \right)dxdy}=\int\limits_{-2}^{1}{dx}\int\limits_{{{x}^{2}}}^{2-x}{\left( x{{y}^{2}}+y \right)dy}$

$\displaystyle =\int\limits_{-2}^{1}{\left[ \left. \left( \frac{x{{y}^{3}}}{3}+\frac{{{y}^{2}}}{2} \right) \right|_{{{x}^{2}}}^{2-x} \right]dx}$

$\displaystyle =\int\limits_{-2}^{1}{\left[ \frac{x{{\left( 2-x \right)}^{3}}}{3}+\frac{{{\left( 2-x \right)}^{2}}}{2}-\frac{{{x}^{7}}}{3}-\frac{{{x}^{4}}}{2} \right]dx}=-\frac{63}{8}$

---

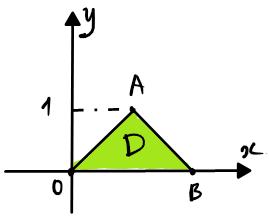
Câu 4. Tính $\displaystyle I=\iint\limits_{D}{\left( xy+y \right)dxdy}$ với miền $D$ là tam giác $OAB$ với $O\left( 0;0 \right)$, $A\left( 1;1 \right)$, $B\left( 2;0 \right)$

+) Biểu diễn miền $D$ trên $Oxy$

Dễ thấy $OA:y=x$ và $AB:y=-x+2$

+) Viết lại $D:\left\{ \begin{align} & 0\le y\le 1 \\ & y\le x\le 2-y \\ \end{align} \right.$

Vậy

$\displaystyle I=\iint\limits_{D}{\left( xy+y \right)dxdy}=\int\limits_{0}^{1}{dy}\int\limits_{y}^{2-x}{\left( xy+y \right)dx}$

$\displaystyle =\int\limits_{0}^{1}{\left[ \left. \left( \frac{{{x}^{2}}y}{2}+xy \right) \right|_{y}^{2-y} \right]dy}$

$\displaystyle =\int\limits_{0}^{1}{\left[ \frac{y{{\left( 2-y \right)}^{2}}}{2}+y\left( 2-y \right)-\frac{{{y}^{3}}}{2}-{{y}^{2}} \right]dy}=\frac{2}{3}$

---

ĐỔI THỨ TỰ LẤY TÍCH PHÂN

Đôi khi việc tính tích phân theo biến này trước sẽ dễ hơn biến kia, do vậy ta phải linh hoạt trong việc thứ tự lấy tích phân để việc tính tích phân bội hai một cách dễ dàng

Câu 5. Tính $\displaystyle I=\int\limits_{0}^{1}{dy}\int\limits_{y}^{1}{{{e}^{{{x}^{2}}}}dx}$

Việc tính tích phân $\displaystyle \int\limits_{y}^{1}{{{e}^{{{x}^{2}}}}dx}$ là phức tạp nên ta đổi thứ tự lấy tích phân

+) Miền $D:\left\{ \begin{align} & 0\le y\le 1 \\ & y\le x\le 1 \\ \end{align} \right.$

+) Biểu diễn miền $D$ trên $Oxy$

+) Viết lại miền $D:\left\{ \begin{align} & 0\le x\le 1 \\ & 0\le y\le x \\ \end{align} \right.$

Vậy

$\displaystyle I=\int\limits_{0}^{1}{dy}\int\limits_{y}^{1}{{{e}^{{{x}^{2}}}}dx}=\int\limits_{0}^{1}{dx}\int\limits_{0}^{x}{{{e}^{{{x}^{2}}}}dy}$

$\displaystyle =\int\limits_{0}^{1}{\left( \left. {{e}^{{{x}^{2}}}}y \right|_{0}^{x} \right)dx}$

$\displaystyle =\int\limits_{0}^{1}{x{{e}^{{{x}^{2}}}}dx}=\frac{1}{2}\int\limits_{0}^{1}{{{e}^{{{x}^{2}}}}d\left( {{x}^{2}} \right)}=\left. \frac{1}{2}{{e}^{{{x}^{2}}}} \right|_{0}^{1}=\frac{e-1}{2}$

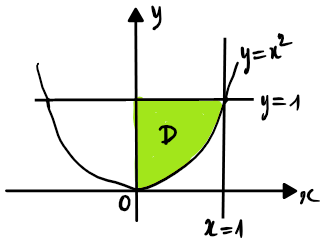
Câu 6. Tính $\displaystyle I=\int\limits_{0}^{1}{dx}\int\limits_{{{x}^{2}}}^{1}{x{{e}^{{{y}^{2}}}}dy}$

+) Miền $D:\left\{ \begin{align} & 0\le x\le 1 \\ & {{x}^{2}}\le y\le 1 \\ \end{align} \right.$

+) Biểu diễn miền $D$ trên $Oxy$

+) Viết lại miền $D:\left\{ \begin{align} & 0\le y\le 1 \\ & 0\le x\le \sqrt{y} \\ \end{align} \right.$

Vậy

$\displaystyle I=\int\limits_{0}^{1}{dx}\int\limits_{{{x}^{2}}}^{1}{x{{e}^{{{y}^{2}}}}dy}=\int\limits_{0}^{1}{dy}\int\limits_{0}^{\sqrt{y}}{x{{e}^{{{y}^{2}}}}dx}$

$\displaystyle =\int\limits_{0}^{1}{\left[ \left. \left( \frac{{{x}^{2}}{{e}^{{{y}^{2}}}}}{2} \right) \right|_{0}^{\sqrt{y}} \right]dy}$

$\displaystyle =\frac{1}{2}\int\limits_{0}^{1}{y{{e}^{{{y}^{2}}}}dy}$

$\displaystyle =\frac{1}{4}\int\limits_{0}^{1}{{{e}^{{{y}^{2}}}}d\left( {{y}^{2}} \right)}$

$\displaystyle =\left. \frac{1}{4}{{e}^{{{y}^{2}}}} \right|_{0}^{1}=\frac{e-1}{4}$

Câu 7. Đổi thứ tự lấy tích phân $\displaystyle I=\int\limits_{0}^{{}^{\pi }/{}_{2}}{dx}\int\limits_{0}^{\sin x}{f\left( x,y \right)dy}$

+) Miền $D:\left\{ \begin{align} & 0\le x\le \frac{\pi }{2} \\ & 0\le y\le \sin x \\ \end{align} \right.$

+) Biểu diễn miền $D$ trong $Oxy$

+) Viết lại miền $D:\left\{ \begin{align} & 0\le y\le 1 \\ & \arcsin y\le x\le \frac{\pi }{2} \\ \end{align} \right.$

Vậy

$\displaystyle I=\int\limits_{0}^{{}^{\pi }/{}_{2}}{dx}\int\limits_{0}^{\sin x}{f\left( x,y \right)dy}=\int\limits_{0}^{1}{dy}\int\limits_{\arcsin y}^{{}^{\pi }/{}_{2}}{f\left( x,y \right)dx}$

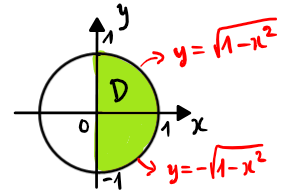
Câu 8. Đổi thứ tự lấy tích phân $\displaystyle I=\int\limits_{0}^{1}{dx}\int\limits_{-\sqrt{1-{{x}^{2}}}}^{\sqrt{1-{{x}^{2}}}}{f\left( x,y \right)dy}$

+) Miền $D:\left\{ \begin{align} & 0\le x\le 1 \\ & -\sqrt{1-{{x}^{2}}}\le y\le \sqrt{1-{{x}^{2}}} \\ \end{align} \right.$

+) Biển diễn miền $D$ trong $Oxy$

+) Viết lại miền $D:\left\{ \begin{align} & -1\le y\le 1 \\ & 0\le x\le \sqrt{1-{{y}^{2}}} \\ \end{align} \right.$

Vậy

$\displaystyle I=\int\limits_{0}^{1}{dx}\int\limits_{-\sqrt{1-{{x}^{2}}}}^{\sqrt{1-{{x}^{2}}}}{f\left( x,y \right)dy}=\int\limits_{-1}^{1}{dy}\int\limits_{0}^{\sqrt{1-{{y}^{2}}}}{f\left( x,y \right)dx}$